How Do You Know if the Data Is Biased
Identifying Bias in Data using Two-Distribution Hypothesis Tests
2021
Overview
Imagine you're flipping a coin you assume to be fair. You flip it 20 times and encounter the sequence $$H T T H T T H H H H H T H T H T H H T H.$$ Zilch immediately stands out to you, so you lot never question whether the money is fair or not. But imagine you flipped that same money and saw the sequence $$H H H H H H H H H H H H H H H H H H H H.$$ You lot'd immediately suspect something was up. More than specifically, you'd near assuredly say that the coin was unfairly weighted towards heads. But how did y'all come up to this conclusion? Was it based on probability alone? If the coin was truly fair, both of the heads-tails sequences higher up have exactly a \(1/two^{20}\) chance of happening, and then what makes you suspicious of the second sequence?
Humans are pretty expert at recognizing patterns, and that very design recognition probably gave you a hint that a weighted coin generated the 2d sequence. Information technology wasn't but the depression probability of that specific sequence occurring that raised your eyebrows. It was as well that sequence's conformity to some pattern. Our team is interested in making use of these 2 factors, probability and conformity, to analyze auto learning training information, and identify the potentially biased processes that could take generated them.
Bias in Artificial Learning
Artificial intelligence (AI), and specifically auto learning (ML) techniques, take become wildly popular in the past decade for making all kinds of applications from phonation assistants to TV show recommendations. In many cases, the faults of an algorithm may not have any sort of meaningful impact. Perhaps yous'll have to endure from a bad Netflix recommendation, merely nothing more than. Even so, ML algorithms are also used to make much more important decisions, like whom to rent at a company or whom to grant a loan to. In these cases, any undesirable beliefs of the algorithm, such equally favoring ane group over some other, will have major consequences. In fact, a few years ago, Amazon had to scrap an entire recruiting tool because it exhibited bias against female person applicants.
How tin can such behavior arise? Algorithms larn from training data, bundles of information virtually thousands of different people or scenarios forth with the correct decision for that datapoint. For a hiring algorithm, this might be information from the applicant'south resume, some demographic data, and a record of whether they were hired or not. However, if that training data had a disproportionate corporeality of white males, for instance, the algorithm may pick up on that and unjustly favor those kinds of applicants over others. Equally such, the upshot of both identifying and eliminating bias in grooming data has garnered a massive amount of attending in recent years, and we hope to contribute to the identification side of this using statistical hypothesis testing.
Project Background
Statistical hypothesis tests allow people to probabilistically rule out a proposed hypothesis every bit an caption for a given dataset. For example, a binomial test could be used to test the hypothesis that our money in the previous case was fair. Such hypothesis tests work by generating a \(p\)-value, the probability that the observation (or a more extreme effect) would occur under the proposed hypothesis. Typically, if this \(p\)-value is less than some called significance threshold alpha, then we reject the null hypothesis. Otherwise, nosotros fail to pass up it.
Several popular hypothesis tests, such as binomial, chi-squared, and Pupil's t, are widely used for testing the plausibility of null hypotheses. Some of these could exist applicable for identifying bias in machine learning training data. Say a company, like the one in the previous section, wanted to train an algorithm to automate their hiring procedure. They would want to be able to feed this algorithm an applicant's demographic data, background, and qualifications and accept information technology return a result of "rent" or "not hire". In club to railroad train this model, they make up one's mind to employ their current and past hiring records, where each current or past applicant has an data profile, and a binary characterization of "hired" or "not hired". Unfortunately, the company suspects that their historical hiring records might exist unjustly biased towards white applicants. Hither we take bias to be deviation from some proposed unbiased explanation. In this example, the unbiased explanation is that racial demographics of the hired employees of the company lucifer that of the unabridged pool of applicants, so no favor is shown to one race over another in the hiring process. A statistical hypothesis test (specifically a chi-squared test in this case) could be used to determine whether this unbiased explanation would plausibly explain the demographics of the hired applicants. By plausible, we mean that the hypothesis was non rejected by the test, not necessarily that the hypothesis has a "loftier" hazard of producing the data.
While all the hypothesis tests mentioned above are useful, all of them presume that sequences are generated under a particular known distribution. This distribution is usually merely the name of the test. For a chi-squared examination, nosotros assume a chi-square distribution. Additionally, these tests can tell you whether or not the proposed hypothesis could plausibly explain the data, but unfortunately do not provide whatever further insight. In many cases, if someone's proposed hypothesis was rejected, they would probably be interested in answering the question of what hypothesis would not be rejected. For the company mentioned above, if their proposed unbiased caption was rejected, they may wonder what caption(s) would not exist rejected, and how close their proposed hypothesis was to such an caption.
That's where our enquiry comes in. Previous piece of work from our lab has generated a novel hypothesis exam that resolves the issues discussed in a higher place. We extend this work and testify useful, existent-world applications of this engineering science for manufacture use.
Key Definitions and Methodology
Define the kardis \(\kappa(x)\) of issue \(x\) every bit $$\kappa(x) := r\frac{p(10)}{\nu(x)}.$$ where \(p(x)\) is the probability of observing \(x\) under probability distribution \(P\) (which represents the zilch hypothesis), \(\nu(x)\) is the specificity (conformity to a pattern) of \(10\) by some predetermined notion of structure, and \(r\) is a normalizing abiding. Find that this formulation of \(\kappa(10)\) captures both the probability and conformity of an issue as discussed earlier.
With this in listen, our lab has shown that for some chosen significance level \(\alpha\) $$\Pr(\kappa(x) \leq \alpha) \leq \alpha.$$ Thus, we can reject a proposed hypothesis \(P\) if \(\kappa(ten) \leq \alpha\). Furthermore, it has also been shown that in order for any new hypothesis to not be rejected by our test, it must boost \(p(x)\), the probability of observing \(x\), by at least a factor of $$southward = \frac{\alpha\nu(ten)}{rp(x)}.$$ This bound is the key to our results, since it means that a proposed probability distribution (explanation) \(Q\) must give at least $$q(x) \geq sp(10)$$ probability to \(x\) in order to not be rejected by our hypothesis test.
Near importantly, this bound allows us to notice the "closest plausible explanation" for the data in the instance that the original proposed hypothesis is rejected by solving a constrained optimization problem. In other words, if a proposed hypothesis is rejected, we can say that the true explanation would have to be biased by at least a certain amount. This gives our test a unique degree of clarity, since it allows users to get a better sense of what hidden biases might exist present in the processes that created their data.
Information technology should exist stated clearly that we are not making claims about bias of whatever particular automobile learning algorithm, or even identifying algorithmic bias at all. Rather, nosotros seek to uncover biases in the processes that generate grooming data, like hiring practices or weighted coins.
Selected Results
Nosotros tested our methods on three existent-globe datasets, two of which will be shown hither. The showtime dataset we tested for bias in was the publicly available COMPAS (Correctional Offender Management Profiling for Culling Sanctions) dataset which was used to train the COMPAS algorithm. The algorithm's purpose was to assign defendants in court a take a chance score for backsliding (trend to reoffend), and it remains a popular tool for judges and parole officers.
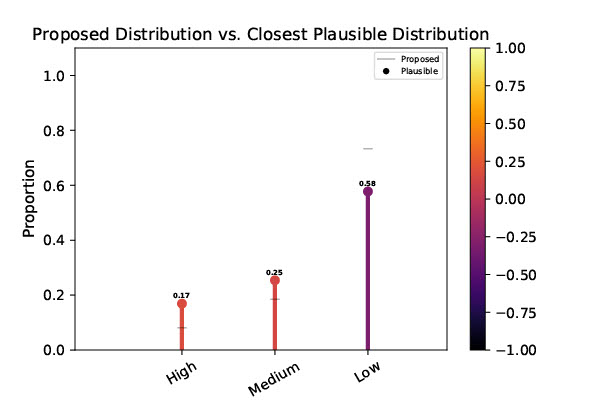
It is already well known that the algorithm is biased confronting Black defendants, consistently giving them unjustly high recidivism scores compared to Caucasians. Our contribution is quantifying the bias in the grooming data itself, and returning a closest feasible caption for this bias. Beginning, we took the proportion of Caucasians assigned to the 3 possible categories: depression, medium, and loftier risk. Since the data is supposed to be fair, we apply these proportions every bit the null hypothesis to test for bias in the Black population. That is, could the same process that generated the Caucasian proportions plausibly have generated the proportions of Blackness people assigned to each category?
As expected, the null hypothesis was rejected at the \(\blastoff = 0.05\) significance level, with a \(\kappa(10)=2.4272 \times 10^{-683}\). Furthermore, we establish that the closest plausible explanation for the information shows Black people having roughly double the probability of being categorized equally "high risk" than Caucasians, which is illustrated in the graph below. The colors of the lollipop confined representing the closest plausible distribution correspond to how far away they are from the proposed distribution, with a heatmap key on the correct.
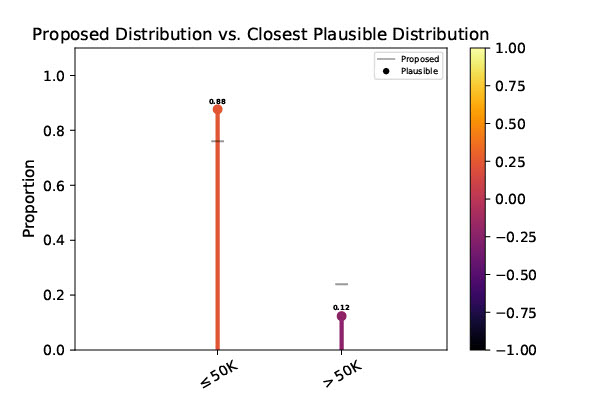
Nosotros also tested the UCI Adult dataset which contains a variety of demographic information for over xl,000 people, with a binary label of whether they brand more than or less than $50,000 per yr. If the procedure that generated dataset is fair in the traditional sense of the discussion, then it should have an equal chance of putting a adult female in the "≤50K" category equally a male person. As such, we used the proportion of men labeled "≤50K" (about 0.76) as our null hypothesis and tested the subset of merely women for deviation from this proportion. Again, the cipher hypothesis was rejected at the \(\alpha = 0.05\) significance level, with \(\kappa(x)=two.2022 \times 10^{-254}\). The closest plausible distribution is illustrated beneath, showing that the nearest plausible caption gives women an 88% chance of being assigned to the "≤50K" group, which is clearly biased from the goose egg hypothesis of 76%. Remember, we are not making statements about whatsoever algorithm, but rather a potential process that could have lead to the given labels in the dataset. In this example, that procedure would exist a wide swath of existent societal factors, including gender discrimination.
Our hypothesis tests also accept some meaning benefits compared to existing methods, which we hope will make them fit for manufacture applications.
- Different other tests in the literature, our tests can handle compound hypotheses. That is, they can reject whole sets of hypotheses, rather than just one at a time.
- They are fast and tractable. Even for datasets consisting of 100,000 entries and ten labels, our tests can run in under 10 minutes on a consumer-level laptop. This contrasts other tests in the literature which appear to need enormous compute power.
- With our tests, in that location is no need to know the beliefs of the underlying probability distribution \(P\) in advance, only the probability \(p(10)\) for the atypical event \(x\). This distinguishes our tests from many common hypothesis tests (chi foursquare, binomial, etc.) which assume a distribution'southward shape.
Additional Resources
Authors
Acknowledgements
This research was supported in part past the National Science Foundation nether Grant No. 1950885. Whatsoever opinions, findings, or conclusions are those of the authors alone, and do not necessarily reverberate the views of the National Scientific discipline Foundation.
Further Reading
- Montañez, G. D. (2018). A Unified Model of Complex Specified Information. BIO-Complexity, 2018.
- Hom, C., Maina-Kilaas, A. R., Ginta, Chiliad., Lay, C., and Montañez, G. D. (2021, February). The Gopher's Gambit: Survival Advantages of Artifact-based Intention Perception. In ICAART (1) (pp. 205—215).
- Jiang, H., and Nachum, O. (2020, June). Identifying and Correcting Label Bias in Auto Learning. In International Conference on Artificial Intelligence and Statistics (pp. 702—712). PMLR.
- Taskesen, B., Blanchet, J., Kuhn, D., and Nguyen, V. A. (2021, March). A statistical test for probabilistic fairness. In Proceedings of the 2021 ACM Briefing on Fairness, Accountability, and Transparency (pp. 648—665).
Source: https://www.cs.hmc.edu/~montanez/projects/bias-in-data.html
0 Response to "How Do You Know if the Data Is Biased"
Enregistrer un commentaire